There is a worldwide hunt in the search for options to optimize running performance through reducing the air-resistance among runners, coaches and running scientists.

Cyclists and speed-skaters have been doing this for a long time already by developing optimal aerodynamic conditions (clothing, frames, body position, streamlining, drafting).

In running, there have been a few breakthroughs in capturing air resistance recently. The first came with the development of the new Stryd, which reports the Air Power in real time. The second was the sensational INEOS 1:59 Challenge. In Vienna, Eliud Kipchoge was helped by 41 pacers (5 teams of 7 pacers and 6 reserves) to achieve his magnificent 1:59:40.

In this paper, we will calculate concretely and exactly how big the impact of the wind speed and the wind direction is on the running speed. As an example, we use author Hans, who weights 58 kg and can run a 5K in 18 minutes.

Theory

In our book ‘The Secret of Running’, we have discussed the theory of the air-resistance in various chapters. According to the fundamental laws of physics, the power required to surmount the air resistance P_a (Air Power) is determined by the density of the air ρ (in kg/m³) the air-resistance factor c_dA (in m²), the running speed v (in m/s) and the wind speed v_w (in m/s), as shown in the box.

The figure below shows the Air Power as a function of running speed v at the standard conditions (temperature 20°C, air-pressure 1013 mbar, so ρ = 1.205 kg/m³, c_dA = 0.24 m², no wind, so v_w= 0 m/s).

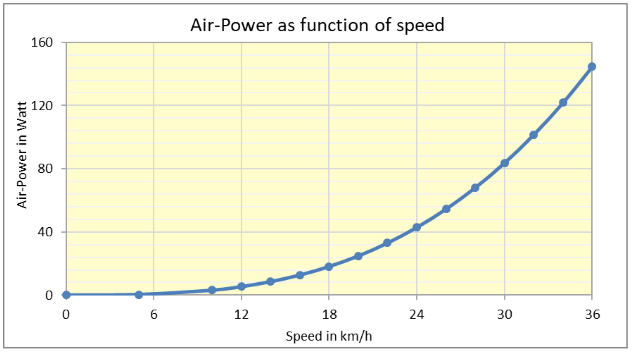
First, we assume that Hans ran his time of 18 minutes in ideal conditions, so no wind (v_w=0).

Consequently, his air-resistance P_a will have been equal to 14 watts at the standard conditions and at his running speed of 5000 / 18 / 60 = 4.63 m/s. His running resistance P_r will have been equal to

4.63 * 58 (kg) * 0.98 (ECOR in kJ/kg) = 263 watts.

How big is the impact of the wind on the air-resistance P_a ?

Next, we have calculated P_a at different wind speeds of 2, 8, and 16 m/s (58 km/h, hard wind with force 7 Beaufort) and both for a headwind and a tailwind. The results are given in the figure below.

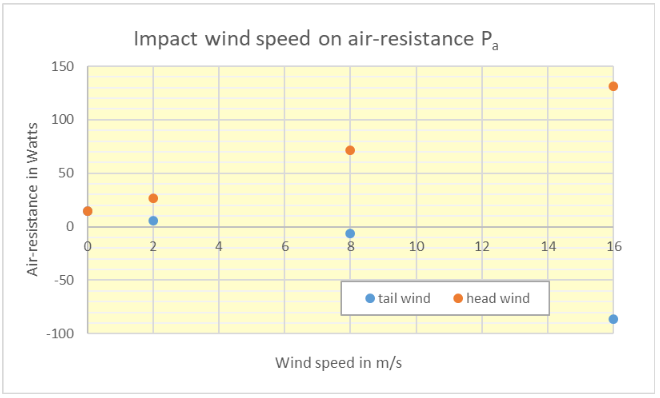
We can see that at a head wind P_a increases from 14 watts to no less than 131 watts, which is almost half of the total power of 277 watts of Hans. At a tailwind, P_a decreases from 14 watts to -86 watts (the negative value indicates he literally gets a push in the back from the wind).

What is the impact on the 5k race time?

We have calculated this from the power balance: P_t = P_a +P_r. Earlier we saw that the P_t of Hans is 277 watts. Consequently, his running power (P_r) decreases as P_a increases (headwind) and vice versa P_r increases as P_a decreases (tailwind.)

The resulting P_r is given in the figure below.

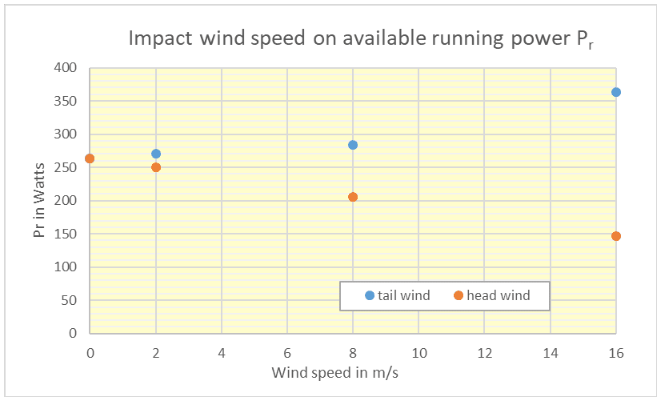
We notice that the available power (P_r) decreases significantly in a headwind (from 263 watts to 146 watts) and increases in a tailwind (from 263 watts to 363 watts).

Of course this has a big impact on the running speed, which can be determined with the formula v (in m/s) = P_r/58/0.98.

Finally, we can calculate the 5K-race time  t (in seconds) from the running speed with the formulae t = 5000/v.

The final result of the 5k-race time is given in the figure below.

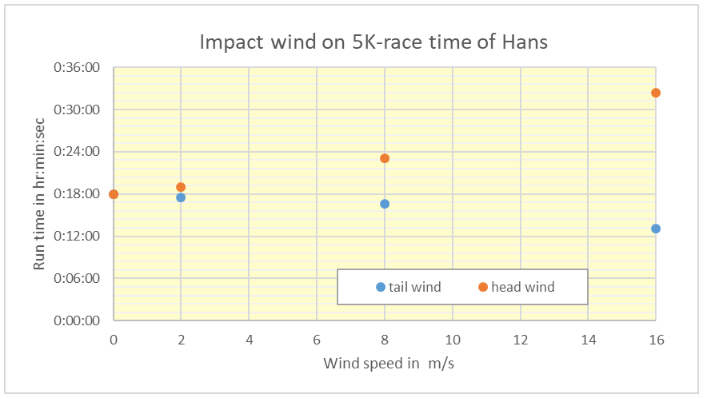
We see that the 5K-race time increases from 18 minutes to more than 32 minutes at a headwind of 16 m/s! With a tailwind of 16 m/s, the race time drops from 18 minutes to just over 13 minutes! If only we could run races with a tailwind of 16 m/s, wow, imagine the record we could set...

And how about the impact of cross wind?

In real running conditions, we never experience a headwind or a tailwind during the whole race. So it is relevant to look at cross winds too. The formulas become more complicated in this case as we have to calculate with vectors of the wind direction and the running direction (the so-called apparent wind). The result is a 6th order polynomial relationship. Our running friend and reader Arno Baels has prepared a spreadsheet to calculate this. In the table below, we show the results for a wind speed of 16 m/s and various wind directions (angles).

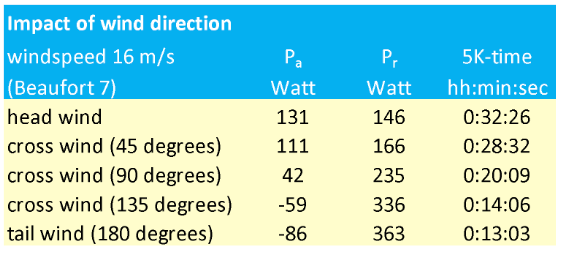
The table clearly shows that the impact is huge at this wind speed. The air-resistance changes significantly at different wind angels and so does the 5K-race time!

Finally, we have calculated the impact on the 5k-race time of a hypothetical race course with 1 K head wind, 1 K cross wind (45 degrees), 1 K cross wind (90 degrees), 1 K cross wind (135 degrees) and 1 K tail wind, This would lead to a race tome of 21:39, so more than 3 minutes slower than at no wind.

We are lucky that Stryd can measure P_a these days!

We feel that the above calculations provide ample arguments to use the new Stryd. At strong winds, P_a will have a big impact on the available running power (P_r) and resulting running speed. Using a Stryd, Hans can just maintain his total power P_t at 277 watts. As a result his pace will automatically go up and down with the wind and he does not have to worry about over or under powering.

How big was the impact of the wind on your race time?

After a windy race, you can use the calculator on our website www.thesecretofrunning.com to get an impression of the time that you could have run in ideal conditions (without wind). It is only an impression as we do not know whether the conditions were variable or you have been able to draft in a pack or in the wake of trees and buildings. In the near future we plan to update our calculator to include the impact of wind directions, as discussed in this paper.

If you would like to purchase The Secret of Running (or the German version, Das Geheimnis des Laufens), you can do so at the bottom of store.stryd.com in the eBook section.